How to check if USB drive is bootable
Ever asked yourself how to test a bootable usb drive without restarting the computer? It’s pretty simple and you don’t need to do much, just follow the next few steps.
- First of all, download this tiny application MobaLiveUSB
- Extract it’s content and copy the executable file to the USB Drive.
- Run as administrator from USB DRIVE (Please note that you have to run the program from the usb drive that you may want to check).
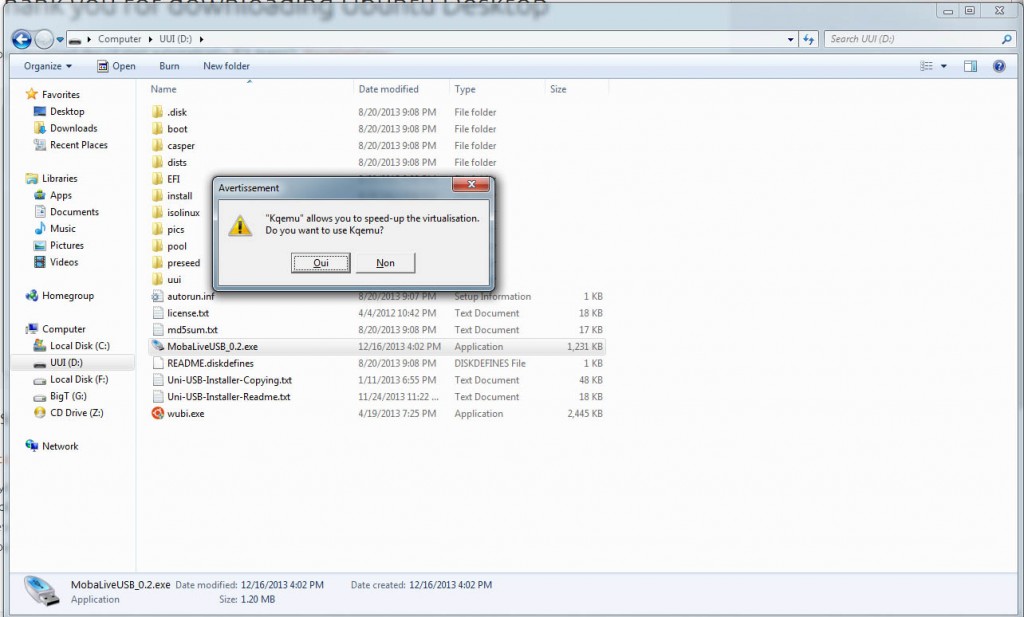
When you run the program it will ask you if you want to use Qemu engine, to boot a virtual machine directly from USB Drive, so please select Oui (*Yes).
That’s it, you don’t have to reboot the machine each time in order to test if your usb drive is bootable or not.

Or use RMPrepUSB which also has QEMU but also has full rd/wr access. QEMU is 32-bit only (there is a 64-bit version but it is not very reliable). It is also slow.
The best utility to use is VirtualBox + DavidB’s Virtual Machine USB Booter app (download from reboot.pro). See http://www.rmprepusb.com/tutorials/how-to-boot-from-usb-under-vmware-server
This is fast (enable CPU VTx support), supports 32 and 64 bit booting and OS’s, and gives full rd/wr access to the USB pen during booting. I use this every day to test USB booting!
LS, Running this tool on a W7 Ultimate 32 bit PC presented a starting screen of Windows which ended in a BSOD.
So questions remains: is my USB drive bootable or not.
sir…i did my pen drive bootable for installing window 7. now i want to make it unbootable. how can ido? please help..
just restore it back to default by formating it
tape this commands
diskpart
list disk
select disk 0 (or 1 or 2…choose the number of your usb)
clean
done
You forgot to type the “create partition primary” command, this is the most important one if you want to create a bootable USB
Just do this:
diskpart
list disk
select disk {number}
clean
create partition primary
select partition 1
active
format fs=fat32 quick
assign
exit
Does NOT work. Won’t copy QEMU files over to the USB drive. So useless.
Sounds like a user error Bob.
Thank you Bill Grates 1971, sohaib & Undernut!
I created bootable usb with rufus. But this tool is not detecting the device as bootable. what should I do?